

First, we calculate P( X ≤ b) and then subtract P( X ≤ a).
What if we want P( X ≤ – x)? Recall that the distribution is symmetric thus,įinally, we might want to calculate the probability for a smaller range of values, P( a < X ≤ b). So, we can still use the tables-look up P( X ≤ x) and then subtract this value from unity. What if we want to calculate probability P( X > x), which corresponds to the non-shaded area in the graph above? Because the probabilities P( X ≤ x) and P( X > x) span the entire sample space (–∞ x) = 1. Typical tables provide probabilities for x values ranging from zero up to three or four (at which point the probability becomes extremely close to unity). Graphically, this probability is also equal to the shaded area shown below. Using Standard Normal Distribution TablesĪ table for the standard normal distribution typically contains probabilities for the range of values –∞ to x (or z)-that is, P( X ≤ x).
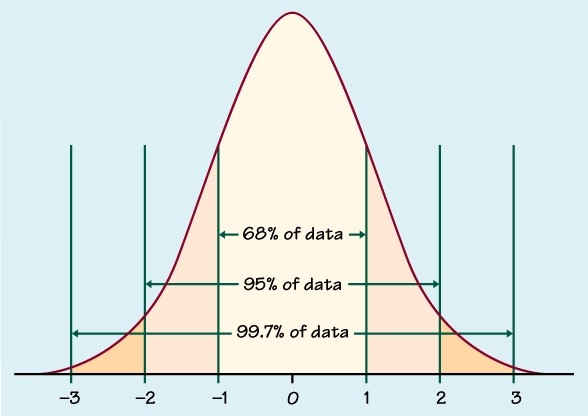
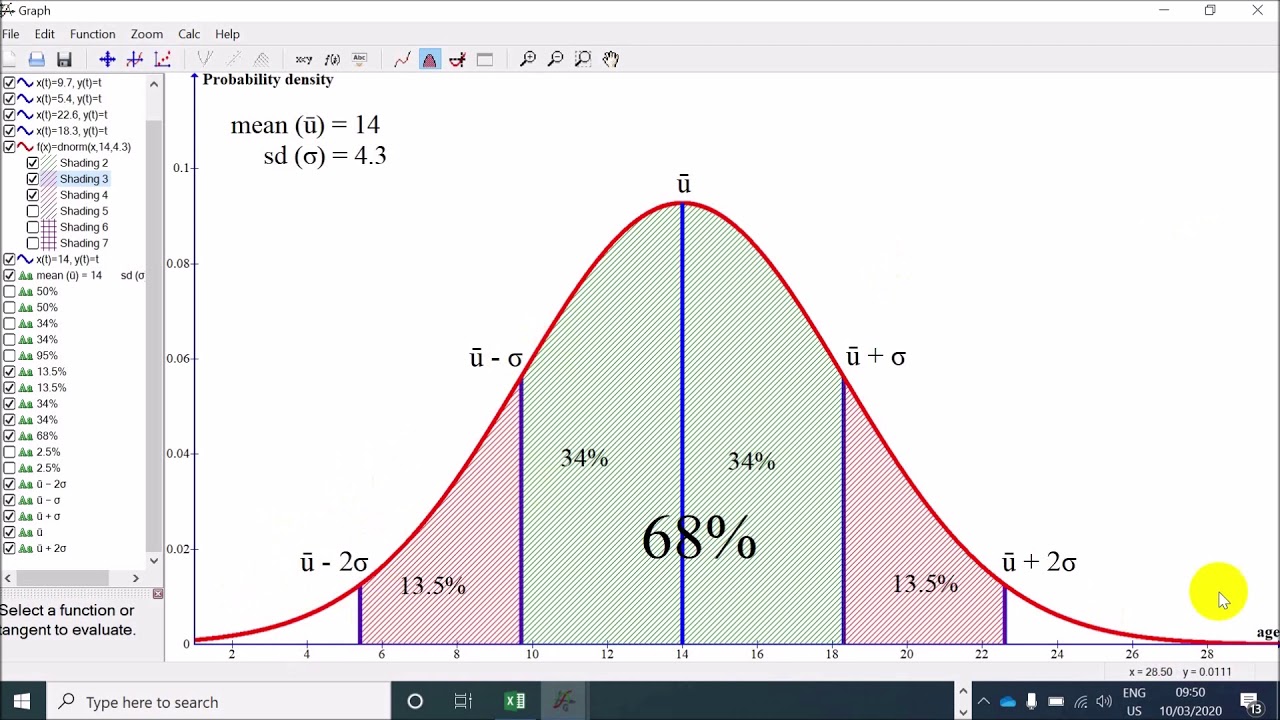
This is a powerful result that allows even those who do not understand integral calculus to calculate probabilities for normally distributed data. Thus, regardless of the details of the problem, we can calculate probabilities for any normal distribution using the standardized distribution. Nevertheless, this process has a particular purpose: because we can standardize a data set from a normal curve with a particular mean and standard deviation to a standardized normal curve with a single mean (zero) and standard deviation (unity), we need only a single table to calculate probabilities for any normal distribution. You might be wondering at this point why we have brought in all the complicated mathematics and seemingly pointless changes of variables. The peak of the curve (at the mean) is approximately 0.399. Note that the standard deviation of the standard normal curve is unity and the mean is at z = 0. The graph of this function is shown below. Out of this transformation falls the standard normal distribution below: Using techniques of integral calculus, we can show that Let's define this expression as z this is also sometimes called the Z-score or standard score. Note in the expression for the probability density that the exponential function involves. Given a situation that can be modeled using the normal distribution with a mean μ and standard deviation σ, we can calculate probabilities based on this data by standardizing the normal distribution. Interested in learning more? Why not take an online Statistics course? The continuous normal distribution cannot be obtained from a sample (because it would require an infinite number of data values). It is important to note that this discussion applies mainly to populations rather than samples. As such, the area under the entire normal curve (which extends to positive and negative infinity) is unity. Recall that a probability for a distribution is associated with the area under the curve for a particular range of values. We can also calculate probabilities of the form P( a < X ≤ b)-in such cases, the shaded region would be more limited. This expression, which calculates the area under the curve from the extreme left (negative infinity) to x = c, refers to the shaded region shown below. Although you need not fully understand the following notation, the probability P( X ≤ x) can be written as Furthermore, the distribution can easily be scaled to conform to the particular mean and standard deviation of interest. Nevertheless, because the normal distribution applies to so many different situations, tables containing probabilities for ranges of values are readily available. The general form of the normal distribution is shown below note the "bell-curve" shape of the graph, and note that the distribution is symmetric about the mean (peak).īecause this distribution is continuous, integral calculus is required to directly calculate associated probabilities. In this formula, μ is the mean of the distribution and σ is the standard deviation. This distribution is known as the normal distribution (or, alternatively, the Gauss distribution or bell curve), and it is a continuous distribution having the following algebraic expression for the probability density. (Be aware that this table is slightly different than the type of table used to solve the problems in the article-the difference is discussed, however.)Ī number of different types of specific distributions have various applications, but one distribution in particular is heavily used (and well known) across a wide range of areas. O A table of values for the standard normal distribution is available at. O Calculate probabilities for normally distributed data
#NORMAL DISTRIBUTION PERCENTAGES PER STANDARD DEVIATION HOW TO#
O Know how to standardize a random variable using the Z-score O Recognize the normal distribution and its fundamental characteristics


 0 kommentar(er)
0 kommentar(er)
